Final Review

Final practice problems

Final Logistics

When and where: December 11 7:00-10:00pm in 75 SHS 102.
What can I bring?: One piece of letter-sized paper with notes on both sides (I will provide copies of the cheat sheet).
What can’t I bring?: Anything else, e.g., book, computer, other notes, etc.
What are office hours this week?: I will generally be in my office from 9:40am - 4pm on Monday (December 8), and then Tuesday (December 9) from 9:30 - 2pm and then Thursday (December 11) from 3 - 5pm.

What will the exam cover?

The exam will effectively have two parts:

Four new questions on the topics covered since Midterm 2 (topics numbered 17-20)
Retake opportunities for all topics from Midterms 1 and 2 (topics numbered 1-16). Recall that you only retake problems for which don’t already have an M (3 points) or E (4 points).

The new topics are:

Searching and sorting algorithms
Use big-O analysis to inform algorithm design
Understand numeric representations and associated operations
Vectorized execution

The retake topics are:

Understand the role of function scope
Writing functions with randomness
Writing functions with loops
Choosing appropriate loops
Creating simpler equivalent conditionals
Finding errors
Writing functions with sequences
Utilizing turtle and other modules
Connect Python to the outside world with file I/O and command line arguments
Implications of the Python memory model
Applications of data structures
Writing functions with sets
Writing functions with dictionaries
Understanding and using recursive functions
Finding errors (in recursive functions)
Using Object-Oriented Programming

The exam may draw from material discussed in class, labs, PrairieLearn problems, quizzes, or programming assignments.

Types of questions

Determine the output/result of code
Rewrite code with better style
Identify bugs in code
Reassemble jumbled Python statements into a viable function
Fill-in missing statements in code
Translate code from NumPy/datascience to “built-in” Python and vice-versa.
Write code to solve a problem
Map algorithms to specific implementations and vice-versa
Determine and compare big-O time complexity and execution time
Plot the result of a vectorized calculation.

Review Questions

Solutions will be available after class (make sure to reload the page).

You are given four programs, each uses one of four different implementation for searching a sorted array: iterative linear search, recursive linear search, iterative binary search, recursive binary search. Unfortunately you don’t know which program uses which approach.
1. Search called with lists of length 433, 432, 431, 430, 429.
2. Search called once with list of length 1000.
3. Search called once with list of length 1000.
4. Search called with lists of length 16, 8, 4, 2, 1
Which program uses which approach?

TipShow a solution

Since search in program A is called with lists decreasing in size by one, we infer recursive linear search. Since search in program D is called with lists decreasing by a factor of 2, we infer recursive binary search. Given the available information, programs B and C could both be iterative linear search or iterative binary search.

If there is insufficient information to answer uniquely suggest an experiment(s) to uniquely identify the approach used by each program.

TipShow a solution

Assuming that search is measurable portion of the runtime and we can change the inputs to the search function, we could try doubling the input size. Since linear search has a time complexity of \(\mathcal{O}(n)\), its runtime should double (or at least increase noticeably), while for binary search as a time complexity of \(\mathcal{O}(\log n)\), and so its run time would only increase minimally.

In practice we could likely observe differences in the absolute run time. But recall the big-O really describes the growth rate as the input grows very large (recall it is described as asymptotic analysis), not the runtime and that two algorithms have the same complexity necessarily mean that they have the same runtime, or if one has lower big-O time complexity that it is predictably faster than the other.
What is the Big-O worst-case time complexity of the following Python code? Assume that list1 and list2 are lists of the same length.
```
def difference(list1, list2):
    result = []
    for val1 in list1:
        if val1 not in list2:
            result.append(val1)
    return result
```
TipShow a solution

The outer loop has n iterations, while the in operation has a worst-case time complexity of n, so the total worst-case time complexity is \(\mathcal{O}(n^2)\).

The not in operator in this context is equivalent to not (val1 in list2). The worst case time complexity for in on a list is \(\mathcal{O}(n)\) because we potentially have to examine all the elements in the list. The average case is still \(\mathcal{O}(n)\), because on average we will need to examine half the elements.

How could we solve this more efficiently? With the subtraction operator on sets.

Why does in use linear search instead of something faster, like binary search? The in operator is designed to work on any list, not just sorted lists. And as we observed in the practice problems, checking if a listed is sorted has the same time complexity as linear search. And so checking first if a list is sorted and then using binary search does not improve our worst case time complexity compared to just using linear search and likely makes the code slower in practice.
What decimal numbers are represented by the following binary numbers:
1. 1101
  
  TipShow a solution
  
  13
2. 111
  
  TipShow a solution
  
  7
3. 10010 + 11011
  TipShow a solution
  1 1 10010 18 +11011 27 ------ -- 101101 45
Translate the following function using NumPy to just use Python built-ins assuming a_list is a list of floats (instead of a NumPy vector) and lower is a single (scalar) float:
```
def sum_above(a_list, lower):
    return np.sum(a_list[a_list > lower])
```
TipShow a solution
Recall that a_list[a_list > lower] is “vectorized” indexing, that is a_list > lower computes a vector (array) of booleans by performing an element-wise comparison. The indexing operation keeps all values of a_list for which the corresponding boolean is True.
def sum_above(a_list, lower): """ Sum all value in a_list greater than lower """ result = 0 for val in a_list: if val > lower: result += val return result
Translate the following code to use NumPy so that it doesn’t use any plain Python for-loops or if statements. Recall the linspace function can be used to create evenly spaced points on an interval. The goal is to calculate n.
```
lst = []
for i in range(101):
    lst.append(i)

n = 0
for x in lst:
    if x ** 2 < 30 * x:
       n += 1
```
TipShow a solution
As suggested, we should first use the linspace function to do the first part. The second part can be achieved by summing the number of values which satisfy the relation.
x = np.linspace(0, 100, 101) n = np.sum(x ** 2 < 30 * x)
The following code estimates \(\pi\) by creating \(n\) random points in a unit square and then determining the number of points (\(m\)) which fall into a quarter circle of radius \(1\). The fraction \(m/n\) is approximately equal to the fraction of the area of this quarter-circle (\(\pi/4\)) to the area of the square. Therefore \(\pi \approx 4 (m/n)\). Translate the code below to using only NumPy (no for-loops or if-statements) and note that np.random.sample(num) returns an array of num random numbers where each number \(r\) is \(0 \le r \lt 1\).
```
import random
n = 100000
m = 0
for _ in range(n):
    x = random.uniform(0, 1)
    y = random.uniform(0, 1)
    if x ** 2 + y ** 2 <= 1:
        m += 1
print("Pi is about " + str(4 * m / n))
```
TipShow a solution
import numpy as np x = np.random.sample(n) y = np.random.sample(n) m = np.sum(x ** 2 + y ** 2 <= 1) print("Pi is about " + str(4 * m / n))

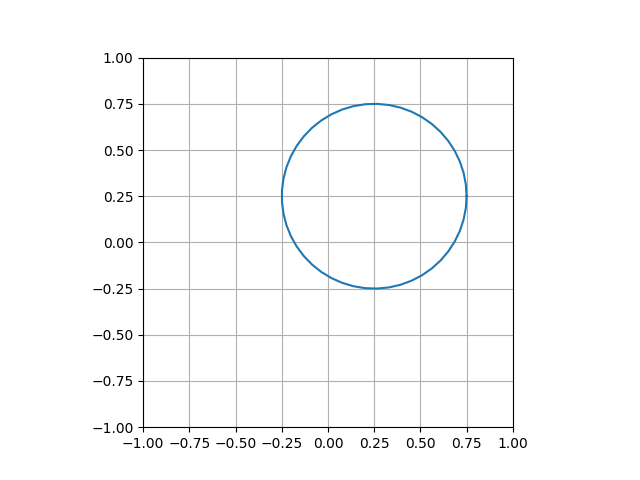
Draw the result of the following numpy and matplotlib code.

import math
import numpy as np
import matplotlib.pyplot as plt

theta = np.linspace(0, 2 * math.pi)
x = 0.25 + 0.5 * np.cos(theta)
y = 0.25 + 0.5 * np.sin(theta)
plt.plot(x, y)
plt.show()

Show a solution

This draws a circle with radius of 0.5 where the center of the circle is (0.25, 0.25).

Sample Exam

Here are Questions 17 - 20 from the Fall 2024 exam. For practice on Questions 1 - 16, please see the previous Midterm reviews (Midterm 1 , Midterm 2) as well as your Midterm submissions on Gradescope.

Fall 2024: exam (only questions 17 - 20), solution