Points
Our first building block is a point, which we'll start by denoting as $\vec{p}$. In 2d this point has two coordinates, $\vec{p} = (p_x, p_y)$, and in 3d a point has three coordinates, $\vec{p} = (p_x, p_y, p_z)$. We'll use parentheses $()$ to delimit the coordinates of a point.
These coordinates represent the distance along the coordinate axes ($x$, $y$ and $z$), measured from some fixed point of origin, which we will take to be $(0, 0, 0)$.
Vectors
A vector is described very similarly to a point, except that it's not measured with respect to a fixed origin. All we care about when describing vectors is the direction and length (along that direction). It might help to think about an arrow that can float around in space: the arrow points in a particular direction (measured from the arrow tail to head) and we can measure its length. In this case, you can think about the tail of the vector as the origin, which can change as we translate the vector around.
Similar to points, vectors are represented using components. We will generally delimit the components using square brackets $[]$. For example, a 3d vector $\vec{u}$ can be described as
$$
\vec{u} = \left[\begin{array}{c}
u_x \\
u_y \\
u_z
\end{array}\right]
$$
where the subscripts denote a particular direction for the component (along the x-, y- or z-axis). Note that we have written this as a column.
Vector addition, subtraction and scaling.
Adding two vectors $\vec{u} + \vec{v}$ produces a new vector $\vec{w}$ whose components is the sum of the components of $\vec{u}$ and $\vec{v}$:
$$
\vec{w} = \vec{u} + \vec{v} = \left[\begin{array}{c}
u_x \\
u_y \\
u_z
\end{array}\right] +
\left[\begin{array}{c}
v_x \\
v_y \\
v_z
\end{array}\right] =
\left[\begin{array}{c}
u_x + v_x \\
u_y + v_y \\
u_z + v_z
\end{array}\right] =
\left[\begin{array}{c}
w_x \\
w_y \\
w_z
\end{array}\right].
$$
Subtraction follows the same idea:
$$
\vec{w} = \vec{u} - \vec{v} = \left[\begin{array}{c}
u_x \\
u_y \\
u_z
\end{array}\right] -
\left[\begin{array}{c}
v_x \\
v_y \\
v_z
\end{array}\right] =
\left[\begin{array}{c}
u_x - v_x \\
u_y - v_y \\
u_z - v_z
\end{array}\right] =
\left[\begin{array}{c}
w_x \\
w_y \\
w_z
\end{array}\right].
$$
Scaling a vector $\vec{u}$ by some scalar $a \in \mathbb{R}$ produces a new vector whose components are $a$ times the components of $u$:
$$
\vec{w} = a\vec{u} = a \left[\begin{array}{c}
u_x \\
u_y \\
u_z
\end{array}\right] =
\left[\begin{array}{c}
a\ u_x \\
a\ u_y \\
a\ u_z
\end{array}\right] =
\left[\begin{array}{c}
w_x \\
w_y \\
w_z
\end{array}\right].
$$
The vector from a point $\vec{p}$ to a point $\vec{q}$ can be computed by subtraction:
$$
\vec{u} = \vec{q} - \vec{p} = \left[\begin{array}{c}
q_x - p_x \\
q_y - p_y \\
q_z - p_z
\end{array}\right].
$$
Length of a vector and unit vectors.
The length of a 3d vector $\vec{u}$ is denoted by $\lVert \vec{u}\rVert$, and is the scalar defined by:
$$
\mathrm{length}(\vec{u}) = \lVert \vec{u}\rVert = \sqrt{u_x^2 + u_y^2 + u_z^2}.
$$
A vector is a unit vector if it's length is 1. Any vector other than the zero-vector (a vector with all zero components, $\vec{0}$) can be normalized to produce a unit vector:
$$
\vec{u}_{\mathrm{unit}} = \frac{\vec{u}}{\lVert \vec{u}\rVert}.
$$
This is scalar division by $\lVert \vec{u}\rVert$ (or multiplication by $1/\lVert \vec{u}\rVert$).
Many vectors in our equations will have an assumption of being a unit vector, so normalization is important!
The dot product.
If we line up two vectors so that their tails coincide, we can label the angle $\theta$ between two vectors $\vec{u}$ and $\vec{v}$:
Imagine we want to compute a new vector that represents "how much of $\vec{u}$ is in the direction of $\vec{v}$?" This vector is equal to $(\lVert \vec{v}\rVert \cos\theta)\vec{u}$, and the overall length of this vector is $\lVert\vec{u}\rVert\lVert \vec{v}\rVert \cos\theta$.
To derive the relationship between the dot product and the angle between vectors, we'll start with the law of cosines:
$$
\lVert \vec{u} - \vec{v} \rVert^2 = \lVert \vec{u} \rVert^2 + \lVert \vec{v} \rVert^2 - 2 \lVert \vec{u} \rVert \lVert \vec{v} \rVert \cos\theta.
$$
Expanding the left-hand-side (LHS) for a 3d vector gives:
$$
\lVert \vec{u} - \vec{v} \rVert^2 = (u_x - v_x)^2 + (u_y - v_y)^2 + (u_z - v_z)^2 = (u_x^2 + u_y^z + u_z^2) + (v_x^2 + v_y^2 + v_z^2) - 2u_xv_x - 2u_yv_y - 2u_z v_z,
$$
which means
$$
\lVert \vec{u} - \vec{v} \rVert^2 = \lVert \vec{u}\rVert^2 + \lVert\vec{v}\rVert^2 - 2 (u_x v_x + u_y v_y + u_z v_z) = \lVert \vec{u} \rVert^2 + \lVert \vec{v} \rVert^2 - 2 \lVert \vec{u} \rVert \lVert \vec{v} \rVert \cos\theta.
$$
The $\lVert\vec{u}\rVert^2$ and $\lVert\vec{v}\rVert^2$ terms on both sides cancel, leaving us with the relationship:
$$
\lVert \vec{u} \rVert \lVert \vec{v} \rVert \cos\theta = u_x v_x + u_y v_y + u_z v_z = \vec{u}\cdot \vec{v},
$$
which is the definition of the dot product. So the dot product is a measure of how much a vector "goes" in the direction of another vector. When the dot product between two vectors is $0$, then the vectors are perpendicular (or orthogonal) - the angle between them is 90 degrees.
The cross product.
We will very (very) often need a vector that is perpendicular to a surface, particularly when we are shading. This vector is often called a normal vector. For simple analytic surfaces, we could figure out an analytic expression for this normal vector, but most geometries in computer graphics are represented using a triangle mesh (a bunch of triangles glued together to represent a surface). For a point on a surface, assume we know which triangle this point is in. Then the normal at this point is the triangle's normal vector.
How do we find this normal vector, which is perpendicular to the triangle? We can use the cross product.
We won't cover the derivation of the cross product and we'll just jump to the definition. The thing we really care about is the fact that the cross product between two vectors produces a vector perpendicular to both vectors. This is what we want in order to shade surfaces.
For 3d vectors $\vec{u}$ and $\vec{v}$, the cross product $\vec{u}\times\vec{v}$ is defined as:
$$
\vec{u}\times \vec{v} = (u_y v_z - u_z v_y)\vec{e}_x - (u_x v_z - u_z v_x)\vec{e}_y + (u_x v_y - u_y v_x)\vec{e}_z
$$
where $\vec{e}_x,\ \vec{e}_y,\ \vec{e}_z$ are the unit vectors along the x-, y- and z-axes, respectively (often represented by $\hat{\imath}, \hat{\jmath},\ \hat{k}$ instead).
As an exercise, show that $\vec{u}\cdot (\vec{u}\times\vec{v}) = 0$ and $\vec{v}\cdot (\vec{u}\times\vec{v}) = 0$.
The cross product can be used to calculate the area of the triangle bounded by vectors along two of the triangle's edges $\vec{u}$ and $\vec{v}$: $\mathrm{area} = \frac{1}{2}\lVert \vec{u} \times \vec{v}\rVert$.
Visualizing the cross product.
The best way to visualize the result of the cross product is to use your RIGHT hand. (1) Start by aligning your index finger with the first vector ($\vec{u}$). (2) Then align your middle finger (or all other fingers) with the second vector $\vec{v}$, moving towards your palm. Your right thumb will point in the direction of the cross-product $\vec{u}\times\vec{v}$.
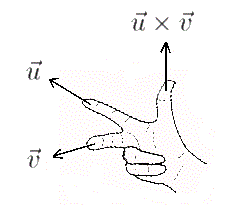
It's import to move your fingers towards your palm in Step (2), otherwise you'll end up with the reversed orientation.
Representing lines.
When we talk about ray tracing (soon), we'll represent rays as lines that emanate from a point into a particular direction. Thus, the following represents the set of all points along a line:
$$
\vec{x} = \vec{p} + t\vec{r}, \quad \forall t \in \mathbb{R},
$$
where $t$ is a scalar parameter, $\vec{p}$ is a point on the line and $\vec{r}$ is the direction. If we make the restriction $t \ge 0$ then we will only include the points that are "ahead" of $\vec{p}$ (including $\vec{p}$).
Representing planes.
Planes can be represented very similarly to lines: we'll use two vectors $\vec{u}$ and $\vec{v}$ and two parameters $s$ and $t$:
$$
\vec{x} = \vec{p} + s\vec{u} + t\vec{v},\quad \forall s,\ t \in \mathbb{R}.
$$
We require that $\vec{u} \times \vec{v} \neq 0$, otherwise $\vec{u}$ and $\vec{v}$ would be parallel. This brings up an alternative (and often more convenient) way to describe a plane: the set of all points $\vec{x}$ satisfying
$$
\vec{n}\cdot(\vec{x} - \vec{p}) = 0,
$$
where $\vec{p}$ is some point on the plane and $\vec{n}$ is a vector normal to the plane. This works because $\vec{n}$ is perpendicular to the plane, and we're requiring that $\vec{x} - \vec{p}$ (which is in the plane) needs to be perpendicular to $\vec{n}$. It doesn't matter what $\vec{p}$ is, as long as it's some point on the plane.
Representing spaces with a basis of vectors.
The representations we had for lines and planes extends to higher-dimensional spaces - we just need more vectors and parameters. A line is one-dimensional so we just need one vector $\vec{r}$ and one parameter $t$. A plane is two-dimensional so we need two vectors ($\vec{u},\ \vec{v}$) and two parameters ($s,\ t$). We'll call these vectors basis vectors.
These basis vectors are not unique. For example, consider a line parametrized by $\vec{p} + t\vec{r}$. We could use another vector $\vec{r}^\prime$ that is just a scaled version of $\vec{r}$, such as $\vec{r} = s\vec{r}^\prime$. Then our line becomes $\vec{p} + t\ s\vec{r}^\prime = \vec{p} + t^\prime\vec{r}^\prime$ for some $t^\prime = s\ t$.
For a plane, we can even rotate the basis vectors around in the plane, or even change the angle between them (as long as we don't make them parallel). If all the vectors are orthogonal (each vector makes an angle of 90 degrees with every other vector), then we say that the basis is orthogonal. If all these vectors further have the property of being unit vectors, then the basis is orthonormal. In general, it's a good idea to use an orthogonal or orthonormal basis, and it will make our life a bit easier when transforming between spaces. More on this when we talk about matrices next class.
Doing everything with glMatrix.
Instead of writing our own functions to perform the operations above, we'll use a popular library called glMatrix. Functions to become familiar with include:
The trickiest part of getting used to glMatrix is: when calling a function that produces a vector, the output vector is both the return value AND the first argument to the function. For example:
let u = vec3.fromValues(1, 2, 3);
let v = vec3.fromValues(4, 5, 6);
let w = vec3.cross(vec3.create(), u, v);
Notice the use of vec3.create() in the first argument passed to vec3.cross. I'm not entirely sure why the API was designed in this way. My best guess is that it allows you to pass any type that supports array-style access (with some index via []).
This is a very common source of bugs, so when your graphics programs are not working, the first thing you should check is whether you are calling glMatrix functions as expected.
Practice
Use the editor on the left (below) to make your own vectors and points to plot. Any vec2's included in the points array will be plotted as black dots, and any vec2's included in the vectors array will be drawn as blue arrows. By default, the vectors will be drawn with the tail at the origin, but you can specify a custom tail for each vector in order to draw it at a different location (set to undefined if you want to use the origin).
Any errors will be alerted in the webpage. If you want to investigate the contents of a point or vector, you can also use alert or console.log (right-click on the webpage and click Inspect to view the console).
